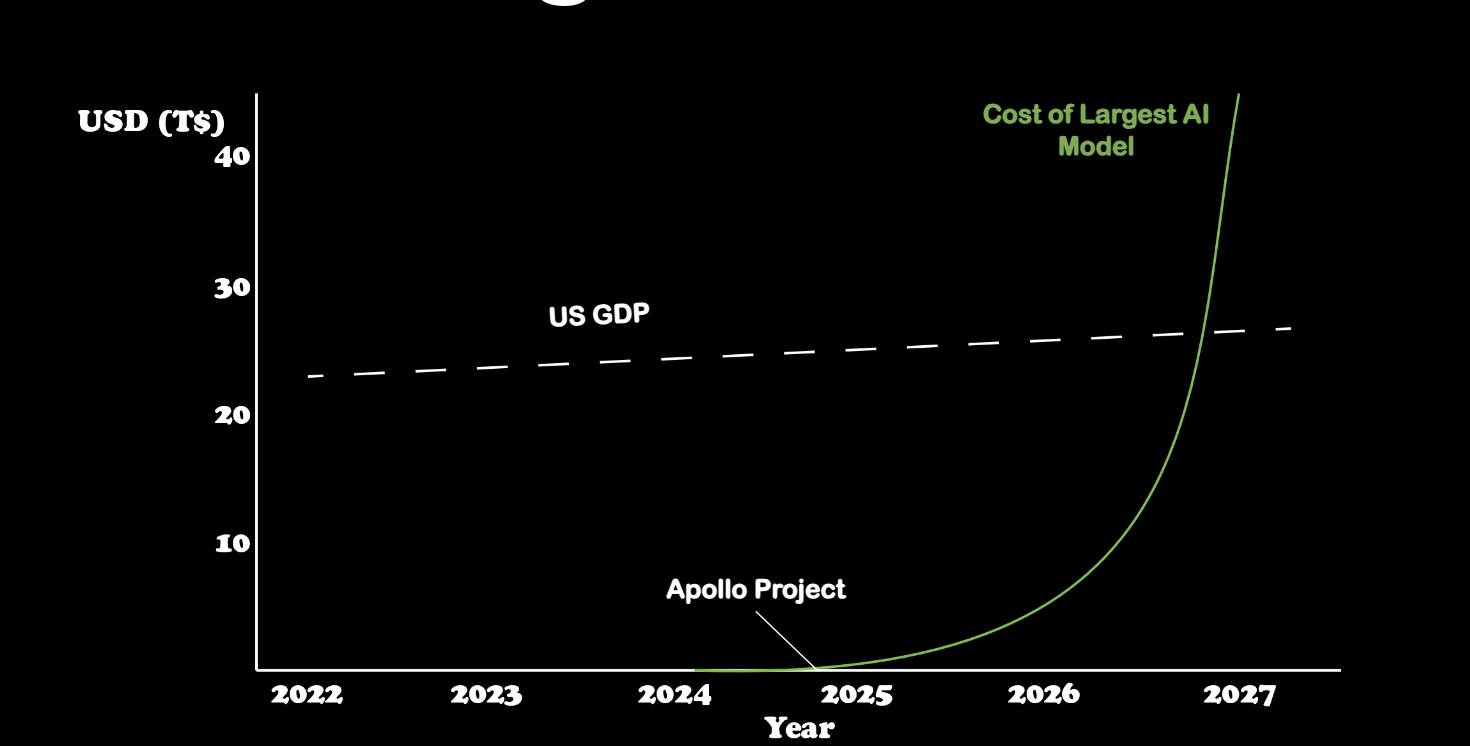
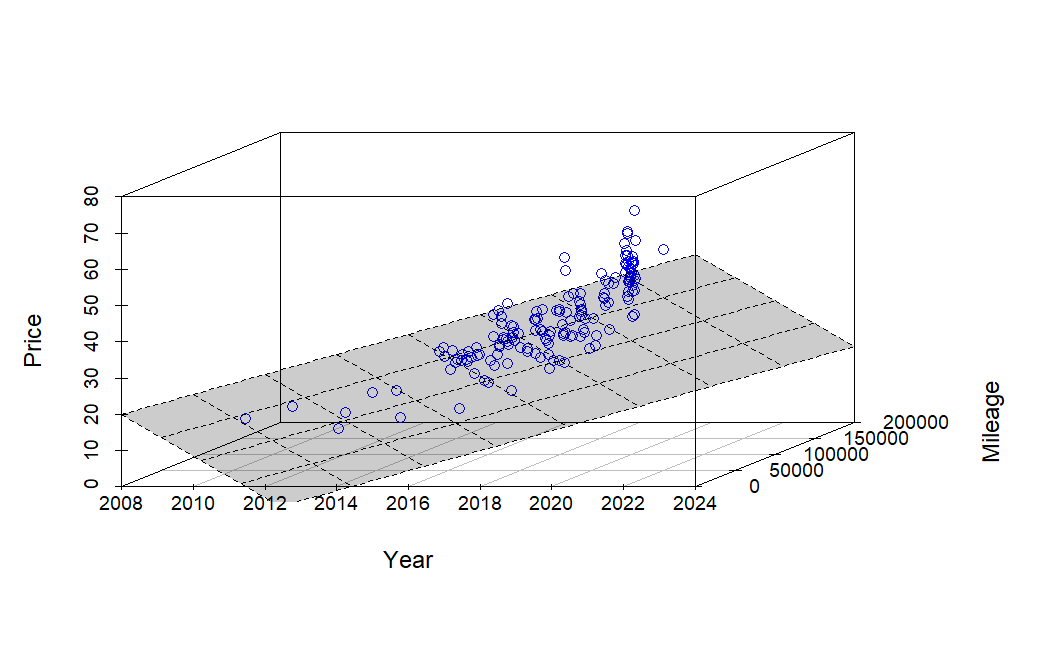
Robots and Chatbots
Before ChatGPT, human looking robotics defined AI in the public imagination. That might be true again in the near future. With AI models online, it’s awesome to have AI automate our writing and art, but we still have to wash the dishes and chop the firewood. That may change soon. AI is finding bodies fast … Read more